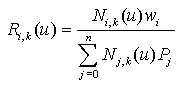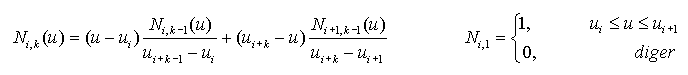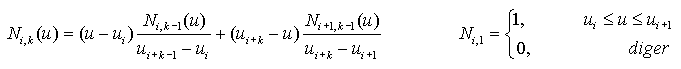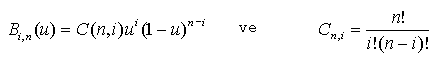Eğriler, analitik ve sentetik  olarak iki gruba ayrılabilir:

Analitik eğriler; doğrular, konik kesitler (çember, elips, parabol, hiperbol), sinüs eğrisi vb. eğrilerdir. Bu eğrilerin analitik bir eşitliği vardır.

Sentetik eğriler ise adından da anlaşılacağı üzere yapay eğrilerdir (Bezier, Hermite Spline, B-Spline, NURBS, vb.). Bu eğriler bir dizi kontrol noktasından belirli bir algoritma vasıtasıyla (interpolasyon veya yaklaşım) hesaplanan eğri noktalarının interpolasyonu ile oluşturulur.

Gelişen teknoloji ve estetik duygulara cevap verecek  ürünlerin dizaynında analitik eğriler yetersiz kalmıştır ve sentetik eğriler geliştirilmiştir. Çevremiz incelendiğinde birçok ürünün sentetik eğrilerle tasarlandığı
görülecektir. Arabalar, gemi gövdeleri, uçak gövde ve kanatları, pervaneler, ayakkabılar, şişeler vb.

NURBS (Non Uniform Rational B-Spline)   eğrileri sentetik eğrilerin en genel hali olarak düşünülebilir. B-spline ve Bezier eğrileri NURBS eğrilerinin özel bir halidir. Ayrıca NURBS eğrilerinin bir avantajı da analitik, doğru ve konik kesitleri tanımlayabilmesidir.

B-spline da Bezier eğrilerinin genelleştirilmiş halidir. Bir Bezier eğrisinin derecesi, kontrol noktası sayısının bir eksiğidir. Yani kontrol noktası sayısı artarsa derece yükselir; Bu da hesaplamaları zorlaştırır. Ayrıca bir kontrol noktasının değişmesi tüm eğriyi değiştirir, yani bölgesel kontrole izin vermez.

NURBS eğrileri, tasarımda ve geometrik şekillere ait verilerinin dönüştürülmesinde endüstri standardı olmuştur. Birçok ulusal ve uluslararası standartlarda (IGES, STEP, PHIGS, vb) NURBS tanımlanmıştır.

NURBS algoritmaları hızlı ve sayısal olarak kararlıdır. Birleştirici matematiksel temeli, hem analitik şekilleri (doğru, konik kesitler, 2. derece yüzeyler, vb) hem de serbest şekilli (yapay) eğri ve yüzeyleri (Araba gövdeleri, uçak gövde ve kanatları, gemi gövdeleri, vb) tanımlayabilmektedir. NURBS; B-Spline ve Bezier, eğri ve yüzeylerini kapsamaktadır.

Doğrusal şekillerin NURBS gösterimi,

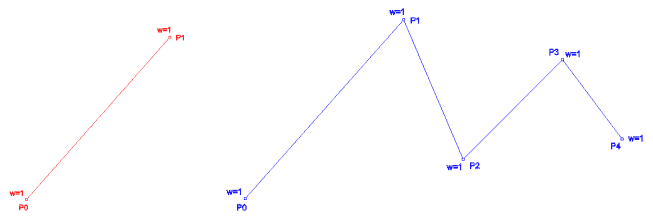
n=1 d=1 kenetli,eşit aralıklı U = { 0,0,1,1}  w = {1,1} 
n=4 d=1 kenetli,eşit aralıklı U = { 0,0,1,2,3,4,4}  w = {1,1,1,1,1} 

Dairesel şekillerin NURBS gösterimi,

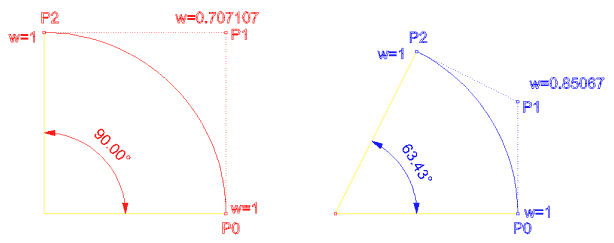
n=2 d=2 kenetli,eşit aralıklı U = { 0,0,0,1,1,1}  w = {1,0.707107,1}
n=2 d=2 kenetli,eşit aralıklı U = { 0,0,0,1,1,1}  w = {1,0.85067,1} 

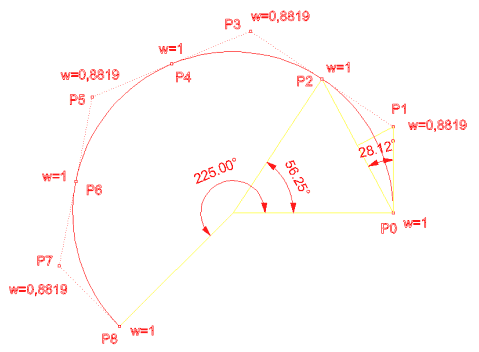
n=8 d=2 kenetli, eşit aralıksız
U = {0,0,0,0.25,0.25,0.5 ,0.5,0.75,0.75,1,1,1}
w = {1,0.8819,1, 0.8819,1, 0.8819,1, 0.8819,1} 

NURBS Tanımı

d. derecede (k. sıra k=d+1),   m+1 bağ dan oluşan bir bağ vektörü  U = { u₀, u₁, .., u_m } ve her biri negatif olmayan ağırlık w_i  (w_i >= 0)  vektörüne sahip bir dizi  (n+1  adet)  kontrol noktası P₀, P₁, P₂ ..., P_n ,  verisi ile bir NUBS eğrisi aşağıdaki şekilde tanımlanabilir.

P(u) : NURBS eğrisi

R_i,k : Oransal B-Spline temel fonksiyonu veya NURBS temel fonksiyonu

N_i,k : B-Spline temel fonksiyonu

P_i : n+1 adet kontrol noktası  P₀, P₁, P₂ ..., P_n

w_i : Kontrol noktasının ağırlığı,  w_i >= 0 

U : Bağ vektörü,  U = { u₀, u₁, ... , u_m-1, u_m }

k : Sıra, k=d+1

d : Derece

R_i,k(u) NURBS temel fonksiyonu:

N_i,k(u) B-Spline temel fonksiyonu:

Bağ vektörünün seçimi

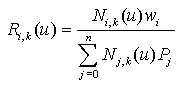
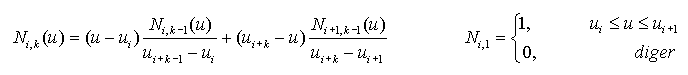
m+1=n+1+k => m=n+k olacak şekilde U = { u₀, u₁, ... , u_m-1, u_m } bağ vektörü oluşturulur.

n=3,k=3 için Bağ Vektörleri

·         Eşit aralıklı ve periyodik bağ vektörü

u_m-u_m-1 =C  dir  U = {0,1,2,3,4,5,6}

·         Eşit aralıklı, periyodik olmayan ve kenetli bağ vektörü

U = {0,0,0,1,2,2,2}  

İlk ve son bağ parametreleri k adet tekrarlanırsa eğri, ilk ve son kontrol noktalarından geçer ve bu tip eğrilere kenetlenmiş eğri denir.

·         Eşit aralıksız (NURBS) bağ vektörü

U = {0,1,2,3,3,3,4} U = {0,0,0,1,2,5,5}

Yukarıda verilen NURBS tanımında eğer tüm w_i =1 ve bağ vektörü eşit aralıklı seçilirse eğri  B-Spline dır.

P(u) : B-Spline eğrisi

N_i,k : B-Spline temel fonksiyonu

P_i : n+1 adet kontrol noktası P₀, P₁, P₂ ..., P_n

U : Bağ vektörü,  { u₀, u₁, ... , u_m-1, u_m }

k : Sıra, k=d+1

d : Derece

N_i,k(u) B-Spline temel fonksiyonu:

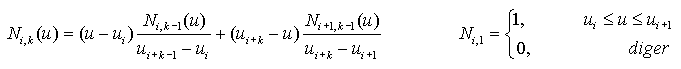
Eğer B-Spline eğrisinin kontrol noktası sayısı  n+1=k  ise eğri Bezier eğrisidir.

Bezier eğrisi aşağıdaki şekilde de tanımlanabilir.

P(u) : Bezier eğrisi

B_i,n : Bernstain temel fonksiyonu

C_n,i : Binominal katsayılar

P_i : n+1 adet kontrol noktası P₀, P₁, P₂ ..., P_n

B_i,n(u) Bernstain temel fonksiyonu:

NURBS Temel Fonksiyonunun Önemli Özellikleri

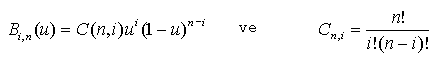
NURBS, B-Spline eğrisinin genel bir hali olduğundan, onun tüm özelliklerine sahiptir. NURBS temel fonksiyonun özellikleri aşağıda açıklanmaya çalışılmıştır.

1.    R_i,k(u) , u parametresine bağlı k-1. dereceden oransal bir fonksiyondur.

2.    Pozitivite; tüm i ve k için , R_i,k(u) pozitiftir.

3.    Bölgesellik; R_i,k(u), [u_i,u_i+k) aralığında sıfırdan farklıdır.
[u_i,u_i+p+1) aralığında N_i,k(u) sıfırdan farklı olduğundan R_i,k(u) da sıfırdan farklıdır. Not: Tüm w_i  lerin negatif olmadığı farz edilmiştir.

4.    Herhangi bir bağ aralığında [u_i, u_i+1), en fazla k adet k-1 dereceli temel fonksiyon sıfırdan farklıdır. R_i-k,k(u), R_i-k+1,k(u), R_i-k+2,k(u), ..., ve R_i,k(u)

5.    Birim Oransallığı; [u_i, u_i+1) aralığında tüm sıfırdan farklı k-1 dereceli temel fonksiyonların toplamı  1 dir.

6.    Bağ sayısı m+1, temel fonksiyonun  derecesi d ve kontrol noktası sayısı n+1 ise m = n + d + 1  veya m=n+k dır.

7.    Temel fonksiyon R_i,k(u), [u_i, u_i+k+1 ) aralığında bağ parametrelerine denk gelen birleşme noktalarıyla bağlanan k-1 dereceli oransal fonksiyonların birleşimiyle elde edilen karma bir fonksiyondur.

8.    s adet tekrarlanan bir bağ noktasında, R_i,k(u) C^k-s sürekliliğine sahiptir.
Bu sebeple, tekrar sayısını arttırmak sürekliliğin seviyesini düşürür ve derece arttırılarak süreklilik seviyesi arttırılabilir.

9.    Tüm i değerleri için w_i = c (sıfırdan farklı sabit) ise, R_i,k(u) = N_i,k(u)
Yani B-Spline temel fonksiyonu NURBS temel fonksiyonunun özel bir durumudur.  

NURBS Eğrilerinin Önemli Özellikleri

NURBS eğrileri B-Spline eğrileri gibi bağ vektörünün seçimine göre açık, kapalı, periyodik veya kenetli olarak sınıflandırılabilir. Bağ vektöründe ilk k adet ve son k adet bağ parametresi eşit seçilirse kenetlenmiş bir eğri oluşur, yani eğrinin başlangıcı, ilk kontrol noktası ve bitişi, son kontrol noktası ile çakışıktır.  

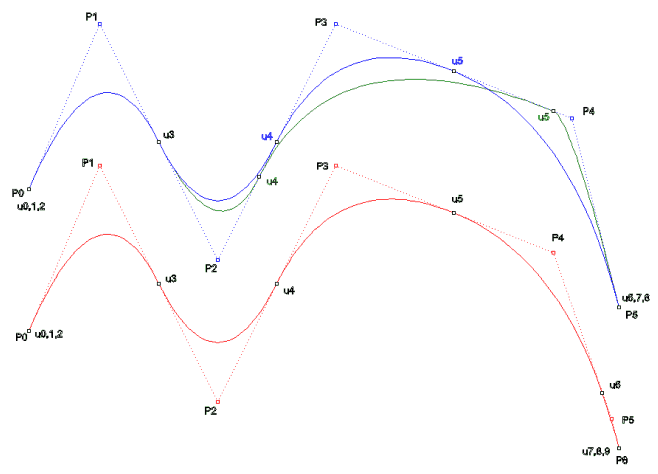
n=5 d=2 kenetli,eşit aralıklı U = {0,0,0,1,2,3,4,4,4} 
n=5 d=2 kenetli,eşit aralıksız U = {0,0,0,1,2,3.843,4,4,4} 
n=6 d=2 kenetli,eşit aralıksız U = {0,0,0,1,2,3,3.843,4,4,4} 

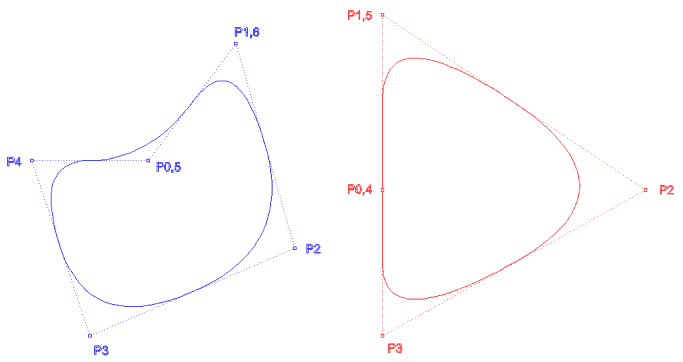
n=6 d=2 kapalı,periyodik,eşit aralıklı U = {-2,-1,0,1,2,3,4,5,6,7}
n=5 d=2 kapalı,periyodik,eşit aralıklı U = {-2,-1,0,1,2,3,4,5,6} 

1.    NURBS eğrisi P(u) , her bir parçacığı k-1. dereceden oransal eğri olan, parçalı bir eğridir. Her bir parçacığa k-1. dereceden Oransal Bezier eğrisi denir.

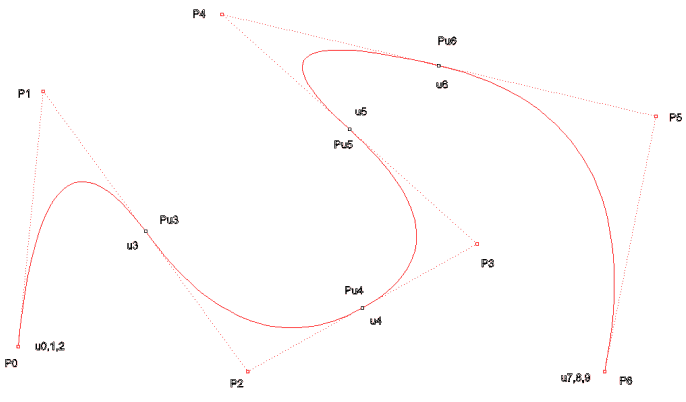
NURBS,n=6 d=2 kenetli,eşit aralıklı U = {0,0,0,1,2,3,4,5,5,5}

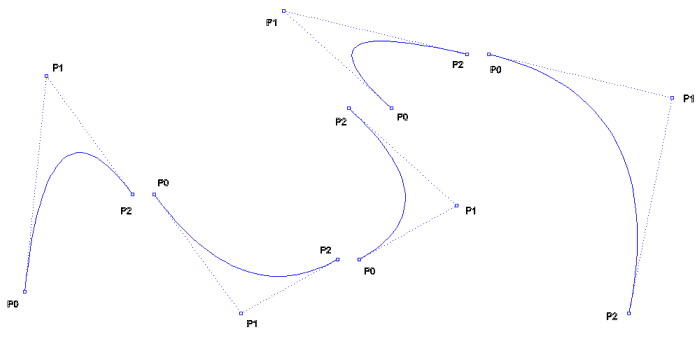
BEZIER Parça Eğrileri; n=2 d=2 kenetli,eşit aralıklı U = {0,0,0,1,1,1} 

2.    m = n + k dır.

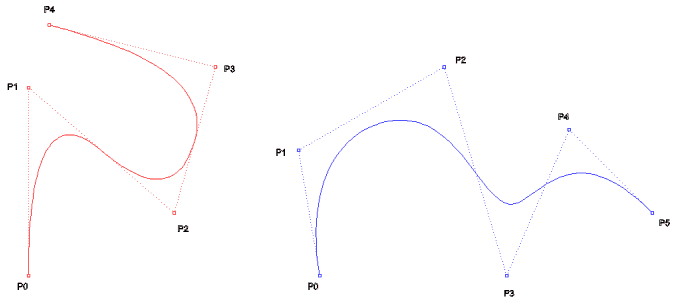
NURBS,n=4 d=2 k=d+1=3 m=n+k=7 kenetli,eşit aralıklı
U = {0,0,0,1,2,3,3,3} 

NURBS,n=5 d=3 k=d+1=4 m=n+k=9 kenetli,eşit aralıklı
U = {0,0,0,0,1,2,3,3,3,3}

3.    Kenetlenmiş bir NURBS eğrisi P(u); P₀ ve P_n kontrol noktalarından geçer.

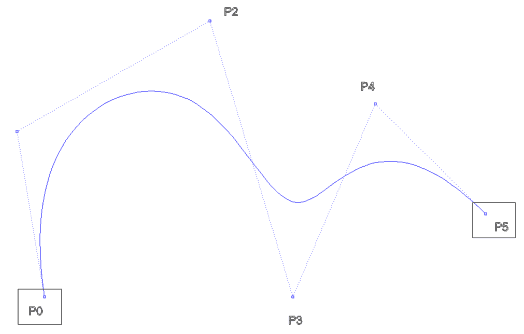
NURBS,n=5 d=3 kenetli,eşit aralıklı U = {0,0,0,0,1,2,3,3,3,3}

Kenetleme için uç noktalarda bağ parametresi k(d+1) adet tekrarlanır.

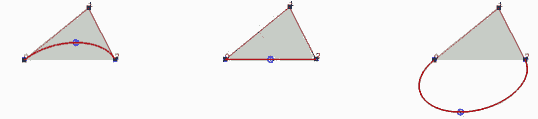
4.    Dışbükey kabuk özelliği; NURBS eğrisi kontrol noktalarının oluşturduğu dışbükey bir kabuk içindedir ve ayrıca eğer  u ; [u_i,u_i+1) aralığında ise P(u); P_i-k, P_i-k+1, ..., P_i  kontrol noktalarının oluşturduğu dışbükey kabuk içindedir. Tüm w_i ağırlıklarının negatif olmaması gerektiğini daha önce belirtilmişti. Eğer bazıları negatif değer alırsa dışbükey kabuk özelliği çalışmaz. Aşağıda soldaki şekilde n=2 ve k=3 olan ve ilk üç ve son üç bağ parametresi kenetlenmiş bir NURBS tür. İlk ve son kontrol noktasının ağırlığı 1 ve ortadaki kontrol noktasının ağırlığı ise 0.5 tir. Bu eğri gerçekte eliptik bir yaydır. Eğri segmenti dışbükey kabuk içinde uzanmaktadır.

Ortadaki şekilde orta noktanın ağırlığı 0 seçilmiştir, bu sebeple bu noktanın eğrinin şekline bir etkisi olmamıştır.Sonuçta doğrusal bir eğri oluşmuştur. Eğri hala dışbükey kabuk içindedir. Sağdaki şekilde ise ağırlık -0.5 olarak seçilmiştir ve eğri  dışbükey kabuğun dışına çıkmıştır.

5.    Bölgesel Düzenleme; P_i kontrol noktasının değiştirilmesi P(u) eğrisini sadece [u_i, u_i+k)  aralığında etkiler. Bu özellik B-Spline temel fonksiyonun getirdiği bir özelliktir. R_i,k(u), [u_i, u_i+k) aralığında sıfırdan farklıdır. Eğer u bu aralıkta değilse R_i,k(u)  sıfır olacağında R_i,k(u)P_i  nin P(u) hesabında bir etkisi olmayacaktır. Diğer taraftan u belirtilen aralıkta ise R_i,k(u)  sıfırdan farklı bir değer alır ve R_i,k(u)P_i  yani P(u) değişir.

Bu özellik eğri dizaynında çok önemlidir. Çünkü eğri, genel şekli değiştirilmeden belirli bölgelerde düzenlenebilir. Eğer daha hassas düzenlemeler yapılması gerekiyorsa bağ vektörüne yeni bağ parametreleri eklenerek eğrinin şekli bozulmadan yeni kontrol noktaları elde edilir. Bu noktaların oluşturulduğu bölgede eğri daha hassas düzenlenebilir.

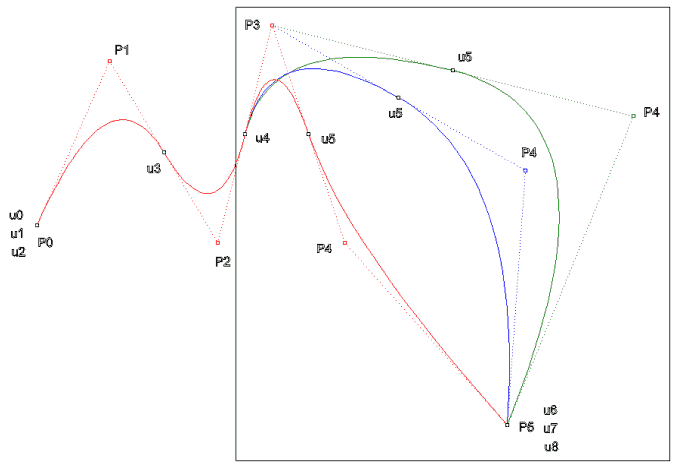
Kontrol noktası değiştirilerek eğrinin düzenlenmesi. P₄ noktası değiştirildiğinde eğri  sadece [u4,u7) aralığında değişir.

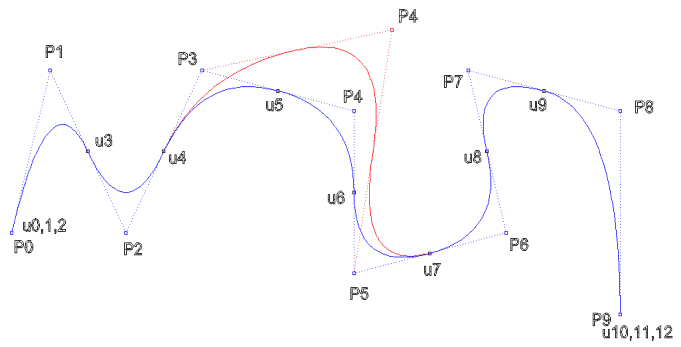
n=9 d=2 kenetli,eşit aralıklı U = {0,0,0,1,2,3,4,5,6,7,8,8,8} 

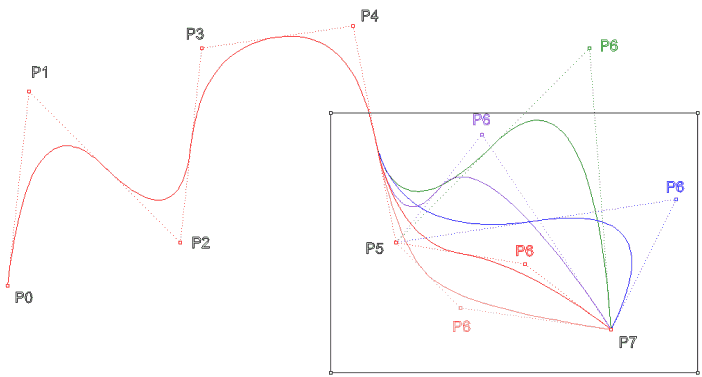
n=7 d=2 kenetli,eşit aralıklı U = { 0,0,0,1,2,3,4,5,6,6,6 } 

Kontrol noktasının ağırlığı (Homojen koordinatlarda 4.boyut) değiştirilerek te  eğri düzenlenebilir. P6 noktasının ağırlığı değiştirildiğinde eğri yine sadece [u6,u9) aralığında değişir.

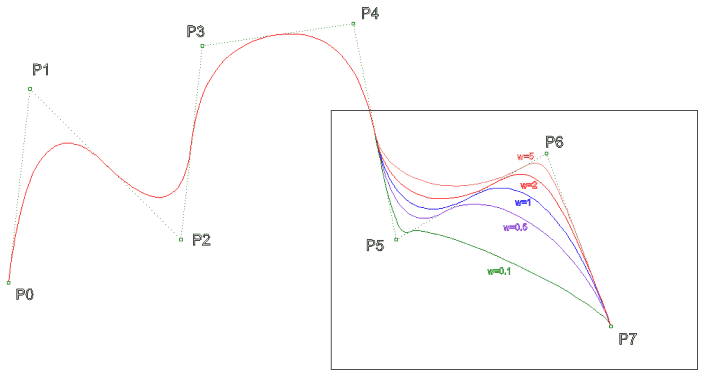
n=7 d=2 kenetli,eşit aralıklı U = { 0,0,0,1,2,3,4,5,6,6,6 }

Mikro düzeyde lokal kontrol için bağ vektörüne yeni bağ parametresi eklenerek eğri şekli değiştirilmeden eklenen bağ parametresine bağlı olarak yeni kontrol noktaları elde edilir. Elde edilen noktaların değiştirilmesi ile eğri o bölgede daha hassas düzenlenebilir. Aşağıdaki şekilde P₄ noktası değiştirildiğinde eğri [u4,u7) aralığında değişmektedir. Eğriyi [u4,u5) aralığında ve P₅ noktasını değiştirmeden düzenlemek için yeni u₆ =3.898 parametresi eklenerek yeni P₄ ve P₅ kontrol noktaları bulunur. Yeni sistemde P₅ kontrol noktası değiştirilerek eğri istediğimiz şekilde düzenlenebilir.

n=5 d=2 kenetli,eşit aralıklı U = {0,0,0,1,2,3,4,4,4}

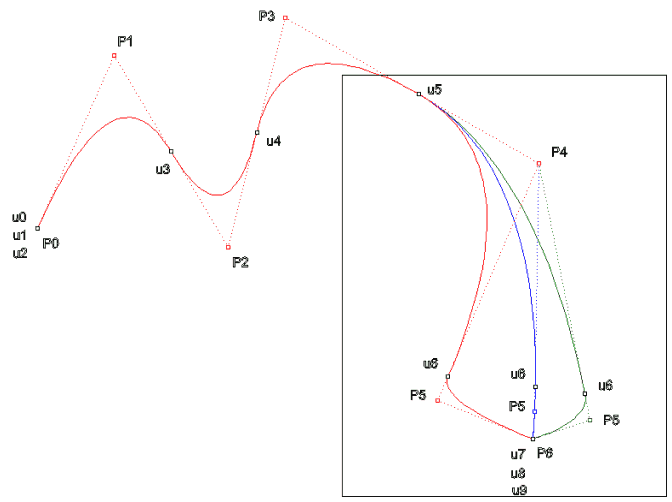
n=6 d=2 kenetli,eşit aralıksız U = {0,0,0,1,2,3,3.898,4,4,4} 

6.    P(u), s katsayılı bağ da C^k-s sürekliliğine haizdir. Eğer u bir bağ parametresine eşit değilse; P(u), k-1 dereceli eğri segmenti üzerindedir ve k-1. seviyeden differanse edilebilir. Fakat u  R_i,k(u) nın sıfırdan farklı bir bağ parametresine eşitse,R_i,k(u) ve P(u),  C^k-s  sürekliliğine haizdir.

7.    Dönüşüm azaltma özelliği; eğer eğri düzlemde (veya uzay) ise eğri ile bir doğrunun (veya düzlem) oluşturduğu kesişimler doğru ile eğri kontrol noktalarının oluşturduğu çoklu doğrunun oluşturduğu kesişimlerden fazla olamaz. (Not: az olabilir.)

8.    B-Spline Eğrileri ve Bezier Eğrileri, NURBS eğrilerinin özel durumlarıdır. Tüm ağırlıklar eşitse bir NURBS eğrisi B-spline eğrisi olur. İlave olarak n = k-1 ise (eğrinin derecesi kontrol noktası sayısının bir eksiği) ve  bağ vektöründeki bağ parametresi sayısı  m=2k-1 ve bağ vektörü kenetlenmiş ise NURBS eğrisi Bezier eğrisine indirgenebilir.

9.    Projektif  değişmezlik; NURBS eğrisine projektif bir dönüşüm uygulanacaksa, sonuç; dönüşümün eğrinin kontrol noktalarına uygulanması ile bulunan yeni noktaların, kontrol noktası olarak kullanılması ile elde edilecek NURBS eğrisidir.

Not: Bezier ve B-spline eğrileri sadece affine değişmezlik özelliğine sahiptirler.